Capacity Expansion Model

1. Overview - What is Capacity Expansion Modelling?

Capacity Expansion Modelling (CEM) is the process of estimating which power plants will be built, retired, or re-powered in the future, and when that will occur. To offer an accurate forecast, we need to model these investment decisions because supply adequacy, wholesale prices, emissions, and system flexibility in 5-25 years’ time all depend on what gets built, not just on today’s fleet. Without an explicit view of future build and retirement choices, long-term price or system outlooks can be wildly misleading.

Why we model future investments:

• Developers and investors chase value. If future prices signal profitable opportunities (for example, high capture prices for solar-plus-storage in a region) projects will queue up.
• Policy and regulation drive build and retirement incentives. Carbon targets, capacity markets, subsidy schemes, tax credits, and planning rules shape what is economic and possible.
• System constraints matter. Transmission limits, interconnection queues, fuel availability, and resource quality (wind/solar resource, CO₂ storage) determine where capacity can be realistically situated.

CEM brings these drivers together so the rest of the forecast (prices, revenues, emissions, reliability metrics) sits on a credible supply-side pathway.

How the model decides “what gets built”

1. Scenario inputs: We start with assumptions for demand growth, fuel & carbon prices, technology costs, policy timelines, and system constraints. These are aligned with the inputs that drive our production cost model.
2. Economic screening: For each technology/location combo, the model estimates its the value of further buildout of that pair.
3. Optimisation / decision logic:
   • Optimization approach: Solve a least-cost capacity expansion problem subject to reliability and policy constraints.
   • Heuristic / rule-based layer: Apply developer behaviour rules (queue attrition rates, build caps, minimum project sizes) to reflect real-world frictions.
4. Co-optimisation with dispatch: New capacity affects prices; new prices affect which capacity is profitable. We simultaneously optimise expansion and dispatch to balance these two factors.
5. Retirements & refurbishments: Units retire when they hit statutory end-of-life limits.

Our Capacity Expansion Forecast runs over a fixed 25+-year horizon (e.g. 2026-2050+). New builds, retirements, and repowers are decided on an annual basis, but each simulated year is dispatched at hourly resolution to capture intraday price swings, flexibility needs, and constraint-driven curtailment. This pairing, annual investment decisions with hourly operations preserves the operational detail needed for credible revenue and reliability outcomes.

2. How the Forecast Works - The Big Picture

Economic optimisation (least-cost, policy-compliant build plan) The model makes investment decisions by minimising total system cost (capex, opex, fuel, carbon, and reliability penalties) subject to demand, reliability, and policy constraints. In practice:

• We feed in demand, fuel/carbon prices, technology costs, and policy targets.
• The optimiser chooses the mix/timing of assets that meets requirements at the lowest net present cost (or, equivalently, maximises system profit under those constraints).

Technology competition (everyone plays by the same rules) Solar, wind, gas, batteries, etc. compete on a comparable economic basis:

• Revenue side: Captured prices from hourly dispatch, ancillary/capacity payments, CfDs, etc.
• Cost/risk side: Capex, fixed/variable O&M, fuel, degradation, cycling costs, financing hurdles.
• Constraints: Resource quality (wind/solar yield), interconnection limits, storage duration, emissions caps. Only technologies that beat alternatives in the optimisation get built.

Real-world planning: rolling window vs. perfect foresight There are two common ways to represent investor planning behaviour:

• Perfect foresight: Assume investors see the entire 25-year future perfectly and optimise once. This is neat but unrealistic.
• Rolling investment window (our approach):
  • Optimise over a shorter forward window (e.g. 5-10 years) using only information “visible” at that decision point.
  • Fix the first decision year’s builds/retirements, roll the clock forward one year, update assumptions (demand, costs, policy changes), and re-optimise the next window.
  • Repeat until the full 25+-year horizon is covered. This captures course corrections, policy shifts, and learning-by-doing, while still producing a coherent long-term pathway.

3. What Drives Investment Decisions

The model’s investment choices are driven by the fundamental economics of power generation: developers and investors build projects where they can earn attractive returns while meeting system needs. Our forecast captures this by modeling how different factors compete to shape the investment landscape over time.

Growing Electricity Demand The primary driver for new capacity is simple: more electricity consumption requires more power plants. As economies grow, populations increase, and new technologies (like electric vehicles and data centers) consume more power, existing generation capacity eventually becomes insufficient. The model tracks projected demand growth and identifies when and where new capacity will be needed to meet future consumption levels.

Aging Infrastructure and Retirements Today’s power plants don’t last forever. As older units reach the end of their economic or technical lives, they retire from the system, creating “replacement demand” for new capacity. The model incorporates realistic retirement schedules for existing plants - whether due to age, poor economics, or environmental regulations - and factors this capacity loss into investment decisions. A retiring 500 MW coal plant in 2030, for example, creates an opportunity for new generation technologies to fill that gap.

Technology Cost Trends Different power generation technologies compete primarily on total cost of ownership. The model considers both upfront capital costs (what it costs to build) and ongoing operational costs (fuel, maintenance, staffing) for each technology:

• Capital costs: Solar and wind costs have fallen dramatically over the past decade, while battery storage costs continue to decline. The model incorporates these trends using authoritative cost projections (such as NREL’s Annual Technology Baseline) to forecast which technologies become more competitive over time.

• Operational costs: Natural gas plants have low capital costs but ongoing fuel expenses that vary with commodity prices. Renewable technologies have higher upfront costs but near-zero fuel costs. The model evaluates these trade-offs across the full asset lifetime.

• Resource quality: A solar farm in Arizona generates more electricity per MW than one in Michigan due to better sun exposure. Similarly, a wind farm in Oklahoma will achieve higher capacity factors than one in Tennessee. The model considers location-specific performance when comparing investment options, ensuring technologies are evaluated based on realistic output expectations.

Financial and Investment Constraints Real-world development doesn’t happen instantly or without limits. The model incorporates several practical constraints that shape investment patterns:

• Annual build limits: There are realistic limits to how much of any technology can be built in a single year due to supply chain, permitting, and construction constraints. You can’t build 50 GW of solar overnight, even if the economics justify it.

• Minimum project sizes: Power plants often have minimum viable scales. A utility-scale solar project typically needs to be at least 20-50 MW to be economically feasible, which the model captures through minimum build requirements.

• Interconnection queue dynamics: Many regions have lengthy queues of proposed projects seeking grid connection permits. The model incorporates this “pipeline” of committed projects and distinguishes between capacity that’s already secured interconnection rights versus new projects that must compete for remaining grid access.

System Reliability and Operational Needs Investment decisions aren’t purely about least-cost generation - the system must remain reliable and operational under all conditions:

• Reserve margins: The grid needs spare capacity beyond peak demand to handle unexpected outages or demand spikes. This reliability requirement can drive investment in dispatchable resources (like natural gas or batteries) even when renewable energy provides the lowest average costs.

• Flexibility and storage: As more variable renewable energy enters the system, the value of flexibility increases. Battery storage, pumped hydro, and other dispatchable resources become more valuable for managing daily and seasonal variability in solar and wind output.

• Geographic distribution: Electricity must be generated near where it’s consumed (unless transmission capacity exists to transport it). The model considers transmission constraints and favors investments that can serve load centers effectively, balancing least-cost resources with practical deliverability requirements.

Policy and Market Structures Government policies and market rules significantly influence investment decisions by changing the relative economics of different technologies:

• Clean energy standards: Renewable portfolio standards, clean electricity standards, and carbon pricing mechanisms can tip the economic balance toward low-carbon technologies by creating additional revenue streams or compliance requirements.

• Tax incentives: Production tax credits, investment tax credits, and accelerated depreciation schedules directly affect project economics and investment timing.

• Environmental regulations: Emission limits, pollution controls, and retirement mandates for older plants create both opportunities (new capacity needs) and constraints (environmental compliance costs) that shape the competitive landscape.

The model integrates these diverse factors through economic optimization: for each potential investment (technology, location, timing), it calculates the total system cost and chooses the portfolio that meets all reliability and policy requirements at the lowest overall expense. This ensures that investment decisions reflect the complex interplay of all factors that drive power sector development.

4. Key Factors That Shape the Forecast

Beyond the economic drivers that create investment opportunities, several practical considerations determine how the forecast actually develops. These factors affect both the credibility of the results and the patterns that emerge in the investment timeline.

Data Quality and Forecast Assumptions The forecast’s reliability fundamentally depends on the inputs that feed into it:

• Technology cost projections: The model uses authoritative databases like NREL’s Annual Technology Baseline to project how costs evolve over time, but different cost scenarios (conservative vs. aggressive learning curves) can significantly change which technologies dominate. Small differences in assumed cost declines can shift the timing of technology transitions by years.

• Resource availability: Rather than using simple averages, the model incorporates detailed weather data that shows how solar and wind output varies hour by hour throughout the year. This detailed approach reveals when renewables complement each other and when the system needs backup power, affecting the mix of technologies that gets built.

• Demand growth patterns: Future electricity consumption isn’t just about total amounts; it’s also about when that consumption occurs. The rise of electric vehicles, data centers, and industrial electrification changes daily and seasonal demand patterns, which in turn affects which types of generation are most valuable.

Geographic and Physical Constraints The physical reality of the power system creates boundaries that shape investment patterns:

• Location matters: The model accounts for the fact that solar resources vary dramatically between sunny and cloudy regions, and wind quality differs between regions. These resource differences mean that identical technologies can have completely different economics depending on where they’re built.

• Grid connection limits: New power plants must connect to existing transmission infrastructure, and some areas have limited remaining capacity for new connections. These physical constraints can redirect investment toward less obvious locations or drive additional transmission investment.

• Real project sizes: Unlike theoretical models that allow fractional investments, the model recognizes that power plants come in realistic sizes. You can’t build a 5.3 MW gas turbine or a 127 MW wind farm because technologies have practical minimum and maximum scales that affect when and where they get built.

Planning Realism and Decision Timing The model captures how real-world planning actually works, rather than assuming perfect foresight:

• Limited planning horizons: Instead of optimizing the entire 25+-year forecast at once (which no real investor can do), the model uses rolling planning windows that reflect how utilities and developers actually make decisions. Early choices affect later options, creating path dependencies that pure optimisation models miss.

• Uncertainty and adaptation: Investment decisions are made based on information available at the time, not perfect knowledge of the future. The model allows plans to evolve and adapt as new information becomes available, producing more realistic investment pathways that respond to changing conditions.

• Interconnection queue realities: Many regions have substantial backlogs of proposed projects seeking grid connection permits. The model distinguishes between this “committed pipeline” and new development opportunities, recognizing that projects with existing permits often have significant advantages over greenfield development.

Operational Detail and System Integration How well the model represents day-to-day system operations affects which investments appear most valuable:

• Hourly operations modeling: Rather than just considering annual energy production, the model simulates how the power system operates hour by hour. This detail reveals the value of flexibility, storage, and dispatchable generation that only becomes apparent when examining daily operation patterns.

• Representative time sampling: Since modeling every hour of every year would be computationally overwhelming, the model uses carefully selected representative periods that capture the key operational challenges - typical days, extreme weather events, and seasonal variations. The choice of which periods to include affects which investments appear necessary.

• System reliability requirements: Beyond just meeting energy demand, the power system must maintain reliability during equipment outages and unexpected events. The model accounts for reserve margin requirements and system flexibility needs that can drive investment in technologies that might not appear economic based on energy production alone.

These practical considerations ensure that the forecast reflects not just economics, but the real-world constraints and decision processes that shape power sector evolution. The model’s design prioritises realistic representation of how investment decisions actually get made.

5. Understanding the Timeline

The capacity expansion forecast is structured around a specific timeline framework that balances long-term strategic planning with near-term decision realism. Understanding this temporal structure is important for interpreting forecast results and understanding how different time periods are treated within the analysis.

25+-Year Forecast Horizon Our capacity expansion forecast spans a 25+-year period, typically from 2026 to 2050, providing a comprehensive view of long-term power system evolution:

Annual Investment Years The model makes capacity expansion decisions on an annual basis, creating discrete investment opportunities each year:

• Annual decision points: Rather than allowing continuous investment throughout the year, the model designates specific investment years (2026, 2027, 2028, etc.) when new capacity can come online. This reflects how real-world development works - projects have specific in-service dates rather than gradual commissioning throughout the year.

• Technology-specific timing: Each technology can have different investment opportunities across years, reflecting factors like manufacturing capacity constraints, supply chain limitations, or policy program availability. A technology might have large build opportunities in some years and limited options in others.

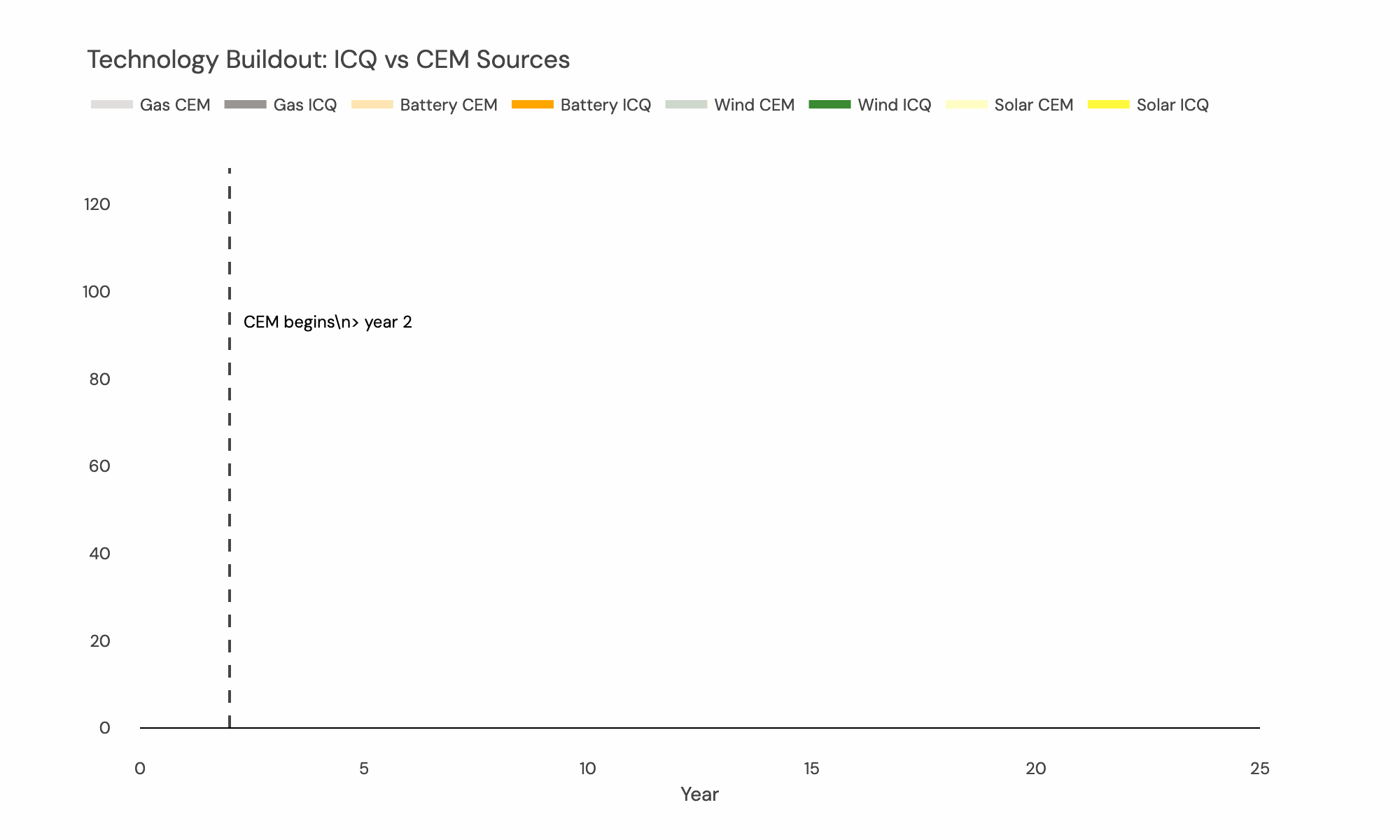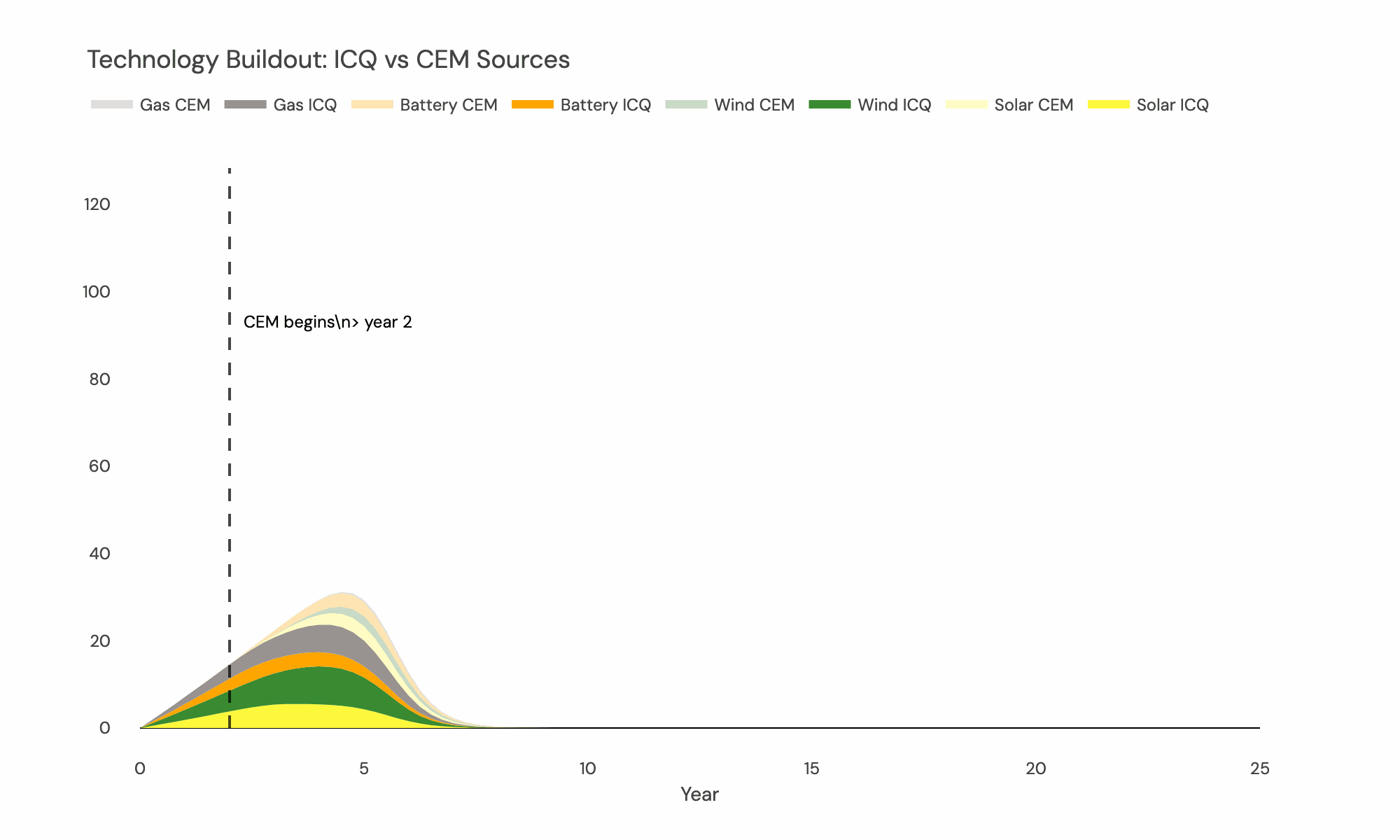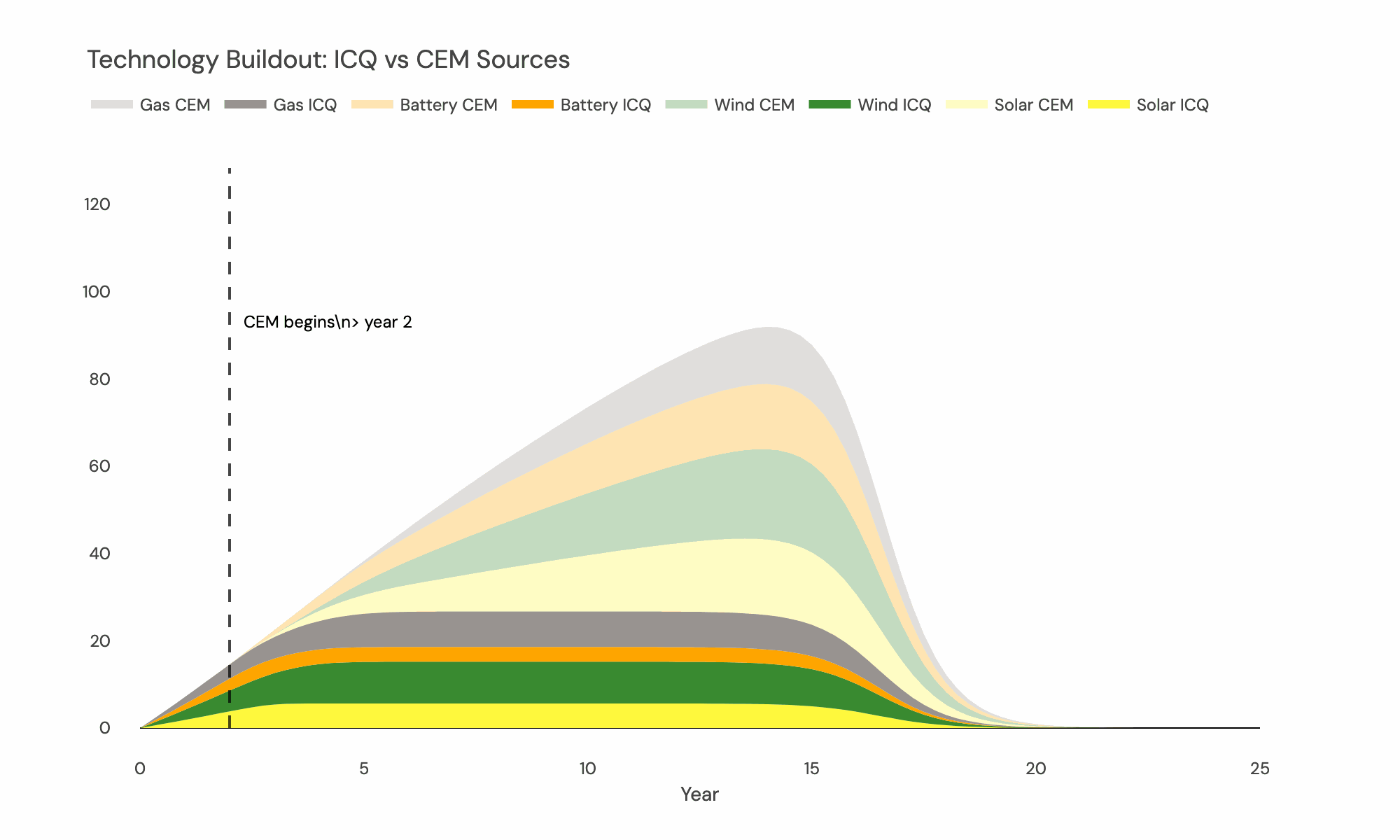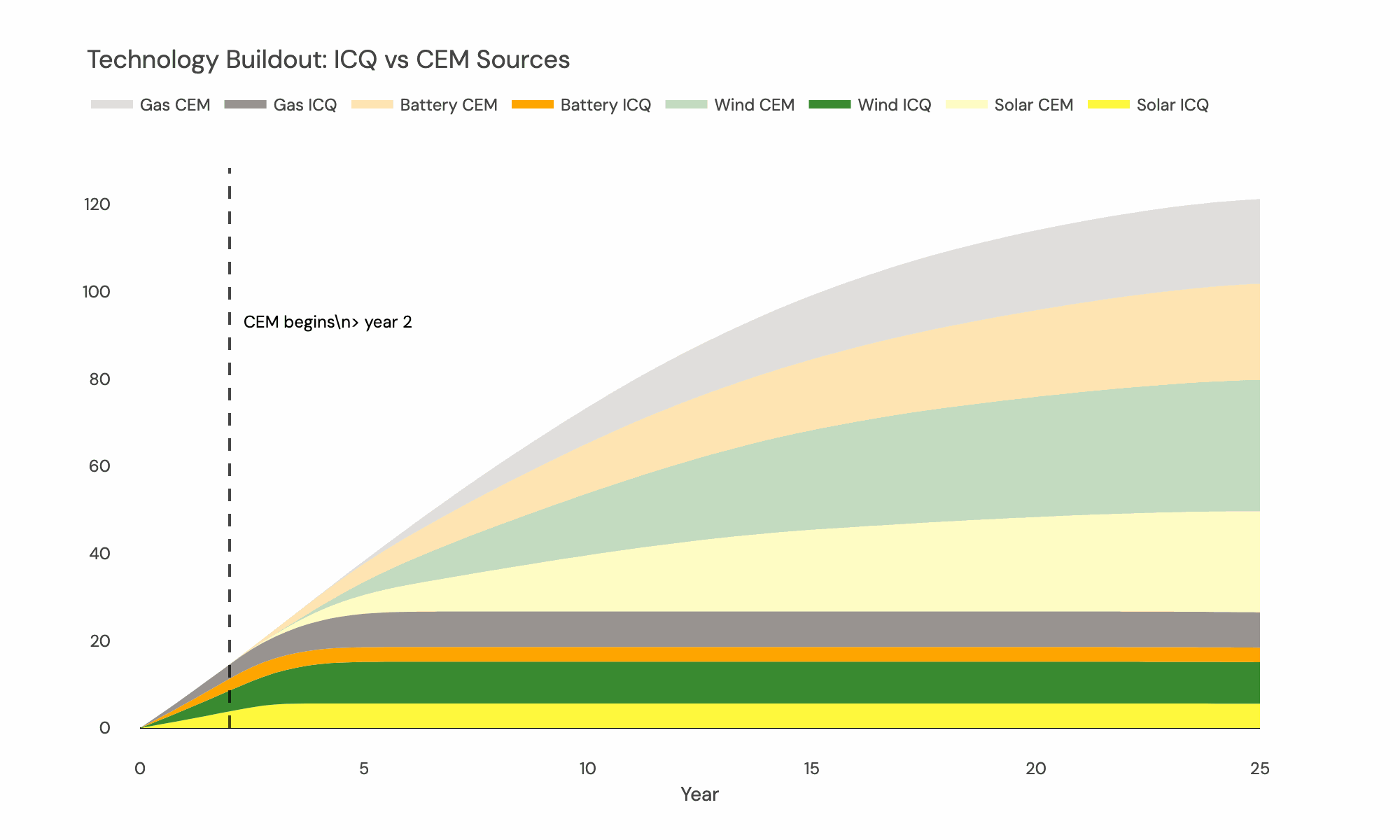
Near-term: Interconnection Queue Foundation The model explicitly incorporates interconnection queue data as fixed capacity additions in the early forecast years:

• Queue data integration: Projects in interconnection queues are input as committed capacity additions with specific in-service years and locations. These projects are treated as fixed additions to the system rather than optimisation variables.

• Queue vs. new-build distinction: The model distinguishes between “ICQ” (Interconnection Queue) capacity that is pre-committed and new optimisation-driven capacity. ICQ projects reduce the available build space for new projects at those nodes/locations and years.

• Queue transition timeline: The relative importance of queue projects versus forecast investments shifts over time. Early years are dominated by queue commitments, while later years have more flexibility for economic optimisation as queue projects represent a smaller share of total additions.

Rolling Window Planning Framework The model uses a specific rolling window methodology with defined parameters:

• Window length: Each planning iteration considers 8 investment years (e.g., 2026 - 2033) in its optimisation. This 8-year window provides sufficient foresight to capture technology cost trends and policy program timelines while remaining computationally manageable.

• Commitment period: From each 8-year optimisation window, only the first 6 years of investment decisions are committed and implemented (e.g., lock in decisions for 2026 - 2031). The remaining years serve as “look-ahead” context but their decisions are reconsidered in subsequent iterations.

• Window progression: After committing the first 6 years, the window advances by 6 years and the process repeats. The second iteration in the example would consider years 2032-2039 and commit decisions for 2032 - 2037, and so on.

• Implementation mechanics: Committed investment decisions from each iteration are physically added to the energy system model as new generation capacity before running the next window’s optimisation. This creates realistic path dependencies where early decisions constrain later options.

6. Types of Technologies Considered

The model evaluates investment opportunities across two main categories of technologies, each with distinct operational characteristics and economic parameters.

Generation Technologies The model optimises investments in dispatchable and non-dispatchable generation options:

• Solar (PVGR): Utility-scale photovoltaic systems with location-specific capacity factors and declining cost trajectories
• Wind: Onshore wind generation with site-specific resource quality and performance profiles
• Natural Gas: Both simple cycle (SCGT) and combined cycle (CCGT) gas turbines providing dispatchable capacity
• Market-specific options: Additional technologies available depending on regional characteristics (offshore wind, biomass, hydro)

Energy Storage Technologies Storage investments are modelled separately with duration-specific parameters:

• Battery storage: Lithium-ion batteries available in multiple duration configurations (1h, 2h, 4h, 6h, 9h)
• Storage operations: Full modelling of charging/discharging cycles, state-of-charge tracking, and efficiency losses
• Grid services: Storage can provide both energy arbitrage and ancillary services like reserves

All technologies compete economically based on their total system value including capital costs, operational costsand the revenue they generate from energy and ancillary service markets.

Excluded Generation Technologies Some generation technologies are not modeled as optimisation variables despite their importance to the power system:

• Nuclear: New nuclear development is primarily driven by government policy decisions and has development timelines (10-15 years) that extend beyond typical market-driven investment horizons. Nuclear investments are typically included as exogenous additions based on announced policy programs rather than economic optimisation.

• Hydro: Large-scale hydro development is constrained by site availability and environmental/regulatory approval processes that operate outside market economics. Existing hydro capacity is modeled but new hydro investments are typically treated as policy-driven additions.

• Hydrogen: Hydrogen generation technologies are still emerging with uncertain cost trajectories and limited commercial deployment. The hydrogen economy infrastructure (production, storage, distribution) requires coordinated development that extends beyond individual generation investment decisions.

These generation technology exclusions reflect that not all power sector investments follow the same competitive economic decision-making processes that drive solar, wind, gas, and storage development. However, where specific projects of these technologies are under development or have committed funding, they are included in the model as predetermined buildout rather than optimisation variables.

7. How the Model Handles Uncertainty

The model must balance computational tractability with operational accuracy when representing full years of hourly operations. Rather than modeling every hour of every year (8,760+ hours annually), the model uses an approach that selects representative periods to capture key system characteristics.

Net Load Calculation and Chunking The representative period selection process begins with calculating net load patterns of the model’s weather year:

• Net load definition: Hourly electricity demand minus variable renewable generation (e.g. solar and wind output)
• Chunk creation: The year is divided into non-overlapping 1-day chunks (365 total chunks per year)
• Chunk characterisation: Each chunk is characterised by three metrics: mean net load, maximum net load, and minimum net load over the 24-hour period

Extreme Period Identification We ensure critical system stress periods and other extremes are always captured:

• Peak demand chunks: The 2 chunks with highest maximum net load are automatically selected to represent system peak conditions
• Low demand chunks: The 2 chunks with lowest minimum net load are automatically selected to represent minimum demand periods
• Extreme period priority: These extreme chunks retain their original weights (typically 1 day each) and are never excluded from representative period selection

Clustering for Representative Periods For the remaining chunks after extreme period selection:

• Similarity grouping: Chunks are grouped based on similarity of their mean, max, and min net load patterns, creating clusters of days with similar characteristics
• Target groups: The number of groups equals the target representative periods minus the extreme periods already selected (e.g. 8-12 groups for 10-14 total representative periods)
• Representative selection: For each group, we select the actual day that is most typical of that group’s average characteristics

The 3D plot below is fully interactive—click and drag to rotate, scroll to zoom, and hover over points to see individual chunk details. Each colour represents a different cluster of similar days.

Weight Calculation and Rebalancing Representative chunks are weighted to preserve annual energy balances:

• Extreme chunk weights: Extreme chunks retain their original weights (number of days they represent)
• Cluster weights: Each representative chunk from clustering receives weight equal to the total original weight of all chunks in its cluster
• Weight normalisation: Total weights sum to 365.25 days to preserve annual energy quantities
• Proportional allocation: Clustered chunk weights are calculated as:

\[w_{\text{chunk}} = \frac{w_{\text{cluster}}}{w_{\text{remaining}}} \times w_{\text{annual}}\]

where \(w_{\text{cluster}}\) is the total weight of all chunks in the cluster, \(w_{\text{remaining}}\) is the remaining total weight, and \(w_{\text{annual}}\) is the remaining annual weight.

• Ordering: The chunks are ordered chronologically to preserve the qualities of the model’s weather year.

Multi-Period Configuration Different forecast periods can use different numbers of representative chunks:

• Near-term detail: Early years (2026-2035) might use 10-12 representative periods for higher accuracy
• Long-term efficiency: Later years (2036-2050) might use 6-8 representative periods for computational efficiency
• Period-specific clustering: Each time period runs independent clustering analysis to capture period-specific demand and renewable patterns

Uncertainty Preservation This methodology preserves key sources of system uncertainty and operational stress:

• Seasonal variation: Clustering captures different seasonal net load patterns throughout the year
• Daily patterns: Each representative chunk includes full 24-hour daily cycles with hourly dispatch optimisation
• Extreme events: Explicit inclusion of peak and minimum demand periods ensures reliability constraints are properly tested
• Renewable variability: Net load calculation captures the interaction between demand patterns and variable renewable output